Pero hoy no voy a hablar de esta peli (si eso algún dia hablaré de alguna teoría matemática), hoy le toca turno a otra peli que encontré después de buscar peliculas matemáticas ^^ Y esta es "Moëbius".
Mmmmm...Moëbius, extraña película sí, la acción sucede en el metro (casi todo el tiempo), está grabada y producida en Argentina (Buenos Aires). La trama consiste en que un día, de repente, desaparece un tren del metro. Desaparece el tren entero y sus pasajeros. Un topólogo (los que estudian las propiedades de los cuerpos geométricos, así a graaaandes rasgos) es contratado para investigar que ocurre.
Este es Daniel Pratt, el cual lleva una investigación del metro, y descubre que la circular (la última ampliación construida) la había echo su antiguo profesor de topología, y que la estructura de la red de metro ahora mismo tiene una superficie infinita, se puede llegar a comportar como una cinta de Moëbius.
(Pulse Leer Mas para continuar artículo).
SPOILER HAGA CLICK PARA VERLO.
Evidentemente, nadie le cree, pero el sigue investigando, y por aquí ahi una escena rarísima a la que todavía no he entendido ni he encontrado ninguna explicación :S viene justo antes de que llegue esta parte:
Pratt se sube a un tren, en el cual ve que en los periodicos pone 4 de Octubre (El día que se perdió el tren), se da cuenta de que está en el tren perdido, y se acerca a la cabina del conductor, donde ¡SORPRESA! Está su profesor.
Sinceramente, por estos 15 minutos de diálogo merece la pena la película, porque es una escena completamente brutal que os transcribo aqui: (Está en Latino)
-Profesor: Le costó llegar ¿no?
-Daniel Pratt: Doctor Mistein.
-P: Cálmese, sé que tienes muchas preguntas para hacer.
-D: Viajamos a una velocidad imposible.
-P: Un simple cambio de vías, el tren cruzó el empalme después de una curva, la convinación justa, el momento adecuado para aplicar las propiedades de una Cinta de Moëbius.
-D: Inventó una máquina perfecta.
-P: No blasfemes, hijo. El hombre ha inventado numerosas máquinas, pero olvida que el mismo es una máquina mucho más complicada que todas las que ha inventado.
-D: Ahora no habrá limites.
-P: Nunca los hubo. El hombre no conoce ni sus límites ni sus posibilidades. Ni si quiera conoce hasta que punto no se conoce. Pero claro, estamos tan ocupados en buscar valores externos, que no nos damos cuenta de lo que realmente importa.
-D: Pero esto es importante. Bastaría con decirlo para que todo cambie.
-P: ¡Pero usted lo dijo! Usted lo explicó perfectamente. Hoy pasé por la estación parque, y lo pude observar detenidamente mientras intentaba explicar la teoría de Moëbius. Jah! ¿Acaso alguien le creyó?
-D: No. Pero a usted le creerían.
-P: No. Yo hubiera usado las mismas palabras que usted, hubiera dicho la misma verdad. Lo que pasa es que vivimos en un mundo donde ya nadie escucha, mi querido Pratt.
-D: ¿Qué piensa hacer con todo esto?
-P: ¡Nada!
-D: ¿Cómo nada?
-P: No se preocupe Pratt, ya llegará el momento.
-D: ¿Y ellos no entienden lo que está pasando? (Refieriendose a los pasajeros del tren).
-P: Ellos... Jamás podrán despertarse antes de haberse dado cuenta de que están dormidos. ¿A qué le teme Pratt?
-D: Al Vértigo.
-P: Es normal. Nadie puede enfrentarse al infinito sin sentir vértigo. Nadie puede experimentarlo sin sentir un desconcierto profundo. Si nos estamos moviendo a la velocidad del pensamiento...
(Aquí vienen imágenes de la gente de los andenes a cámara lenta).
-Profesor: ¿Cómo se podría estar encantado en esta vida, privada de atractivos e ingenuidad, y de espontaneidad? ¿Cómo no preferiría quedarme aquí, en las sombras, si ahí afuera hay un mar de sorderas que nos está arrastrando a ser, irremediablemente desgraciados?
-Daniel: No puede ser que todo esto desaparezca.
-P: Ni los hombres ni el tiempo desaparecen sin dejar huellas. Quedan fijados en nuestras almas.
(Aquí acaba esta escena, no voy a decir como es el final, porque también es sorprendente, pero voy a poner unas palabras que aparecen justo al final de la película):
- Nunca llegué a imaginar lo que al poco tiempo me iba a ocurrir. Cuando alcancé el 86 encontré a mi viejo profesor, ya arto de repetir la misma historia, de luchar y hablar hasta el cansancio, para luego ser ignorado. Y en ese preciso instante sentí que confiaba su tiempo a mis manos. No es dificil comprender porqué he decidido seguir sus pasos en este viaje sin retorno, antes que perder el tiempo tratando de explicar a un grupo de necios aquello que no quieren entender. De cualquier modo, el viejo tenía razon... Vivimos en un mundo donde ya nadie escucha.
Cada uno que saque sus propias reflexiones y conclusiones, yo veo que claramente (a pesar de los 14 años que han pasado desde la realización de la película) vivimos en ese mundo, un mundo donde nadie quiere escuchar nada que no sea lo que él desea oir. Di lo que quiero, o mejor cállate, porque serás tratado de loco, y no te quemaremos como a Galileo, no, simplemente serás ignorado por el resto de la gente, tendrás tratamiento especial con medicamentos. ¿Y todo porqué? Por vislumbrar una realidad que el resto de gente no ve, o no quiere, o no puede.
Una buena película, por lo menos el transfondo, recomiendo verla ^^
Pratt se sube a un tren, en el cual ve que en los periodicos pone 4 de Octubre (El día que se perdió el tren), se da cuenta de que está en el tren perdido, y se acerca a la cabina del conductor, donde ¡SORPRESA! Está su profesor.
Sinceramente, por estos 15 minutos de diálogo merece la pena la película, porque es una escena completamente brutal que os transcribo aqui: (Está en Latino)
-Profesor: Le costó llegar ¿no?
-Daniel Pratt: Doctor Mistein.
-P: Cálmese, sé que tienes muchas preguntas para hacer.
-D: Viajamos a una velocidad imposible.
-P: Un simple cambio de vías, el tren cruzó el empalme después de una curva, la convinación justa, el momento adecuado para aplicar las propiedades de una Cinta de Moëbius.
-D: Inventó una máquina perfecta.
-P: No blasfemes, hijo. El hombre ha inventado numerosas máquinas, pero olvida que el mismo es una máquina mucho más complicada que todas las que ha inventado.
-D: Ahora no habrá limites.
-P: Nunca los hubo. El hombre no conoce ni sus límites ni sus posibilidades. Ni si quiera conoce hasta que punto no se conoce. Pero claro, estamos tan ocupados en buscar valores externos, que no nos damos cuenta de lo que realmente importa.
-D: Pero esto es importante. Bastaría con decirlo para que todo cambie.
-P: ¡Pero usted lo dijo! Usted lo explicó perfectamente. Hoy pasé por la estación parque, y lo pude observar detenidamente mientras intentaba explicar la teoría de Moëbius. Jah! ¿Acaso alguien le creyó?
-D: No. Pero a usted le creerían.
-P: No. Yo hubiera usado las mismas palabras que usted, hubiera dicho la misma verdad. Lo que pasa es que vivimos en un mundo donde ya nadie escucha, mi querido Pratt.
-D: ¿Qué piensa hacer con todo esto?
-P: ¡Nada!
-D: ¿Cómo nada?
-P: No se preocupe Pratt, ya llegará el momento.
-D: ¿Y ellos no entienden lo que está pasando? (Refieriendose a los pasajeros del tren).
-P: Ellos... Jamás podrán despertarse antes de haberse dado cuenta de que están dormidos. ¿A qué le teme Pratt?
-D: Al Vértigo.
-P: Es normal. Nadie puede enfrentarse al infinito sin sentir vértigo. Nadie puede experimentarlo sin sentir un desconcierto profundo. Si nos estamos moviendo a la velocidad del pensamiento...
(Aquí vienen imágenes de la gente de los andenes a cámara lenta).
-Profesor: ¿Cómo se podría estar encantado en esta vida, privada de atractivos e ingenuidad, y de espontaneidad? ¿Cómo no preferiría quedarme aquí, en las sombras, si ahí afuera hay un mar de sorderas que nos está arrastrando a ser, irremediablemente desgraciados?
-Daniel: No puede ser que todo esto desaparezca.
-P: Ni los hombres ni el tiempo desaparecen sin dejar huellas. Quedan fijados en nuestras almas.
(Aquí acaba esta escena, no voy a decir como es el final, porque también es sorprendente, pero voy a poner unas palabras que aparecen justo al final de la película):
- Nunca llegué a imaginar lo que al poco tiempo me iba a ocurrir. Cuando alcancé el 86 encontré a mi viejo profesor, ya arto de repetir la misma historia, de luchar y hablar hasta el cansancio, para luego ser ignorado. Y en ese preciso instante sentí que confiaba su tiempo a mis manos. No es dificil comprender porqué he decidido seguir sus pasos en este viaje sin retorno, antes que perder el tiempo tratando de explicar a un grupo de necios aquello que no quieren entender. De cualquier modo, el viejo tenía razon... Vivimos en un mundo donde ya nadie escucha.
Cada uno que saque sus propias reflexiones y conclusiones, yo veo que claramente (a pesar de los 14 años que han pasado desde la realización de la película) vivimos en ese mundo, un mundo donde nadie quiere escuchar nada que no sea lo que él desea oir. Di lo que quiero, o mejor cállate, porque serás tratado de loco, y no te quemaremos como a Galileo, no, simplemente serás ignorado por el resto de la gente, tendrás tratamiento especial con medicamentos. ¿Y todo porqué? Por vislumbrar una realidad que el resto de gente no ve, o no quiere, o no puede.
Una buena película, por lo menos el transfondo, recomiendo verla ^^
Bueno, una vez fuera de la película (La vayas a ver o no, recomiendo leer lo escrito, pinchando aquí arriba, donde pone Spoiler), vamos a hablar un poco de la Cinta de Moëbius y sus peculiaridades ¿no?
Empecemos por lo que es una cinta, imaginemos un trozo de papel, una tira mejor dicho, y unimos sus dos extremos, tendríamos lo que es una cinta de toda la vida, con dos caras, una exterior, y una interior ¿no?
Si empezamos en un punto, ya sea interior o exterior, continuaremos por esa parte, sin pasar a la contraria en ningún momento.
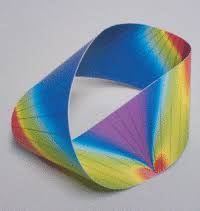
Bien, pues si a esta cinta, justo antes de unir los extremos, damos media vuelta a uno de los dos extremos, tenemos lo que se denomina Cinta de Moëbius. ¿Porqué es tan peculiar esta cinta? Pues porque no existe exterior ni interior, si empiezas en un punto interno y continuas hacia adelante, llegarás a un punto externo, y si sigues más adelante llegarás a un punto interno de nuevo, así indefinidamente, es decir, de una superficie finita, hemos conseguido diseñar una superficie infinita.
Como podemos observar, simplemente el mirarla ya hipnotiza, pero la cinta de Moëbius tiene muchos trucos ocultos para sorprendernos topológicamente.
Por ejemplo:
¿Qué pasaría si cortamos la cinta por la mitad longitudinalmente? ¿Y qué ocurriría si la cortamos en tres, es decir, una vez cortada longitudinalmente, volvemos a cortarla longitudinalmente(muy, muy, muy cuidadosamente)? ¿Y si la cortamos infinitas veces?
Respuestas lógicas naturales: 1) Tenemos dos cintas. 2) Tenemos cuatro cintas (dos por cada una de las anteriores) 3) tendremos 2 elevado a infinito.
Respuestas verdaderas:
1) Tendremos una cinta más grande.
2) Tendremos dos cintas unidas entre sí.
3)Tendremos infinitas cintas unidas entre sí.
E aquí un video representativo:
La Cinta de Moëbius es la estructura básica de la topología infinita, de las cuelas luego hubo muchas más distintas y más complejas, como la botella de Klein.
Si se quiere saber algo más (matemáticamente, ya que yo ni idea, y no voy a hacer copy&paste) de la cinta de moëbius, click aquí.
He hablado (dos parrafos antes) de la botella de Klein, la cual es bastante impresionante, ya que es una botella, sin dentro y sin fuera. ¿Cómo es eso? Pues exactamente así:
Evidentemente, si quieres saber algo más acuda a la querida Wikipedia
/*Vivimos en un mundo donde ya nadie escucha.*/


2 comentarios:
Muy interesante:
Hoy en la Universidad con mis alumnos vamos a hablar de lo importante que es saber escuchar, saber preguntar, y la utilización del "silencio de oro".
Es verdad, uno de los grandes problemas que tenemos hoy es "que vivimos en un mundo en el que nadie escucha". Además hay muchos, demasiados "ruidos"...
Si nos lo proponemos, si empezamos a preguntar de verdad, si nos esforzamos en la escucha de verdad (escucha activa), y si usamos con frecuencia el maravilloso "silencio de oro", ¡todo a nuestro alrededor cambia!
¡Merece la pena!
Luis Mª
Todos deveriamos aprender algo nuevo alguna vez en nuestra corta vida para transmitirlo y perdure para siempre
Publicar un comentario